Mathe macht Spaß Setzten Reiskörner den Fürsten schachmatt?
St. Wendel · In diesen Corona-Zeiten ist immer wieder vom exponentiellen Wachstum die Rede. Was sich dahinter verbirgt, zeigt Mathe-Professor Rainer Roos. Und hat einige Beispiele und Aufgaben parat. Zum Beispiel die Sache mit den Reiskörnern.
Die größte Unzulänglichkeit der Menschheit ist unsere Unfähigkeit, die Exponentialfunktion zu verstehen“, so der amerikanische Physiker und Bevölkerungsforscher Albert Bartlett. Bilder von Exponentialfunktionen haben wir seit Beginn der Corona-Pandemie oft gesehen: die Entwicklung der nachgewiesenen Coronafälle in einer Region. Oder wie hier in Grafik 1 eine Modellrechnung: Wie entwickelt sich die Anzahl der Coronafälle bei einer Verdopplungszeit der Infektionen von zehn Tagen während eines halben Jahres? Zu Beginn gab es eine Infektion. Dazu dann der Kommentar: exponentielles Wachstum.
Exponentielles Wachstum? Was ist das? Wo kommt so etwas vor? Darum geht es heute. Wir fangen mit einem berühmten Beispiel an: Es geht ums Papierfalten. Unsere erste Frage, Ihre erste Aufgabe: Nehmen Sie Ihre Saarbrücker Zeitung. Falten Sie sie einmal, zwei Mal, drei Mal, so oft Sie können. Ich habe es sieben Mal geschafft.
Zeitungspapier ist etwa 0,1 Millimeter dick. Angenommen, man könnte die Zeitung 42 Mal falten, wie hoch würde der entstehende Stapel? Natürlich kann niemand eine Zeitung 42 Mal falten, die faltbare Fläche würde viel zu klein. Nehmen wir einmal an, die Saarbrücker Zeitung hätte die Fläche des Saarlandes, etwa 2500 Quadratkilometer (so klein sind wir!) und würde 42 Mal gefaltet. Die Rundungen an den Faltstellen vernachlässigen wir dabei. Wie groß wäre dann die Stapeloberfläche? Das ist unsere zweite Frage und Ihre zweite Aufgabe.
Übrigens, ein Rekord im Paperfalten wurde 2002 von der englischen Schülerin Britney Gallian aufgestellt, zwölf Faltungen mit einem speziellen Toilettenpapier. Es besteht kaum Gefahr, dass dieser Rekord in der nächsten Zeit gebrochen wird. Mehr über solche Faltungen und ihre Grenzen können Sie bei Clifford Pickover, Das Mathebuch, auf Seite 504 erfahren.
Auch unsere dritte Frage, Ihre dritte Aufgabe ist ein Klassiker: Das berühmte Schachbrettproblem. Hier die Kurzfassung. Der Erfinder des Schachspiels, der Brahmane Sissa ibn Dahir, sollte von seinem Fürsten belohnt werden. Der gewährte ihm einen freien Wunsch. Sissa erbat sich das Folgende: „Lege, oh Herr, auf das erste Feld eines Schachbretts ein Reiskorn, auf das zweite zwei, auf das dritte vier, auf jedes weitere Feld immer das Doppelte bis zum Feld 64.“ Der Fürst lachte und sagte, er wolle das gern tun. Wirklich?
Unsere dritte Bitte, Ihre dritte Aufgabe: Wie viele Reiskörner kommen auf diese Weise zusammen? Die folgende Tabelle soll Ihnen eine kleine Hilfe geben:
Feld Körner Summe
1 1 1 = 2-1
2 2 1+2=3 = 4-1
3 4 1+2+4=7 = 8-1
4 8 1+2+4+8=15 = 16-1
Wir fragen weiter: Wenn das mittelere Gewicht eines Reiskorns 0,025 Gramm beträgt und wenn 2019 etwa 500 Millionen Tonnen Reis geernet wurden, wie viele Weltjahrsernten kommen da zusammen? Exponentielles Wachstum. Sie werden staunen.
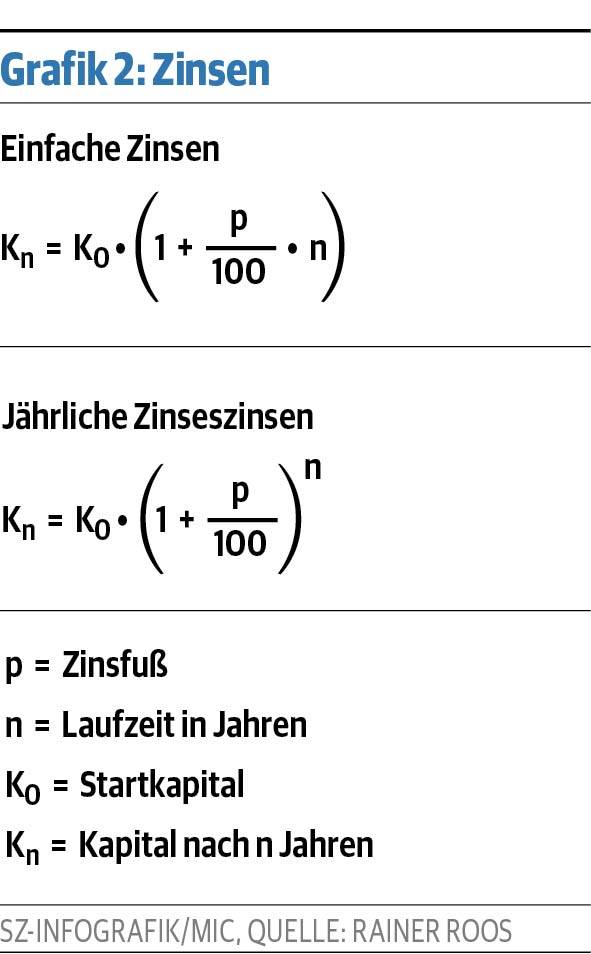
Exponentielles Wachstum spielt auch in normalen Zeiten eine wichtige Rolle, vor allem in der Finanzwelt, wenn es um Zinseszinsen geht. Zinsen kann man auf verschiedene Art berechnen: Es gibt einfache Zinsen und Zinseszinsen. Bei einfachen Zinsen sind die Zinsen proportinal zur Zeit. Das bedeutet zum Beispiel, dass die Zinsen nach zehn Jahren das Zehnfache der Zinsen nach einem Jahr sind. Zinseszinsen funktionieren anders. Sie alle kennen das Prinzip: Am Ende eines jeden Jahres kommen die Zinsen zum Kapital zu Beginn des Jahres und bilden das neue Startkapital.
Die Zinsen, also der Zuwachs, sind immer proportional zu dem aktuellen Bestand. Dies ist das Prinzip eines jeden exponentiellen Wachstums (oder Schrumpfens). Genau so war es am Anfang der Corona-Pandemie.
Woher kommt der Name „exponentielles Wachstum“? Sie sehen es an der Zinseszinsformel. Die Laufzeit n steht im Exponenten. Siehe dazu Grafik 2.
Machen wir am Ende ein Gedankenexperiment. Stellen Sie sich vor, im Jahr 20 nach Christus, in Rom regierte Kaiser Tiberius, lebten zwei Ihrer Vorfahren in Trier. Einer arm und klug, einer reich und nicht ganz so klug. Beide wollten für Sie Geld anlegen. Der arme Schlucker verfügte nur über eine Goldmünze, einen Aureus. Den legte er bei seiner Bank an, zu 1 Prozent jährlichen Zinseszinsen. Der andere legte 10 000 Aurei zu zehn Prozent an, bei einfachen Zinsen. Wir unterstellen 2000 Jahre lang stabile und wirtschaftliche Verhältnisse. Unsere vierte Frage, Ihre vierte Aufgabe: Welche Anlageform bringt heute den größeren Ertrag? Und wie war es im Jahr 1020, als Heinrich II., der letzte Ottone, das Reich regierte?
Am Ende noch eine Einschätzung des anfangs erwähnten Albert Bartlett: Er hielt den Begriff „nachhaltiges Wachstum“ für ein Oxymoron. Unsere letzte Bitte, Ihre letzte Aufgabe: Qxymoron, was ist damit gemeint? Und hat er Recht?